The conspiratorial Monty Hall problem
dynomight.net/conspiratorial-monty-hall
The Monty Hall problem has now been a pox on humanity for two generations, diverting perfectly good brains away from productive uses.
So it is with great trepidation that I’d like to announce a new and more pernicious variant.
Reminder
As a reminder, here’s the standard problem:
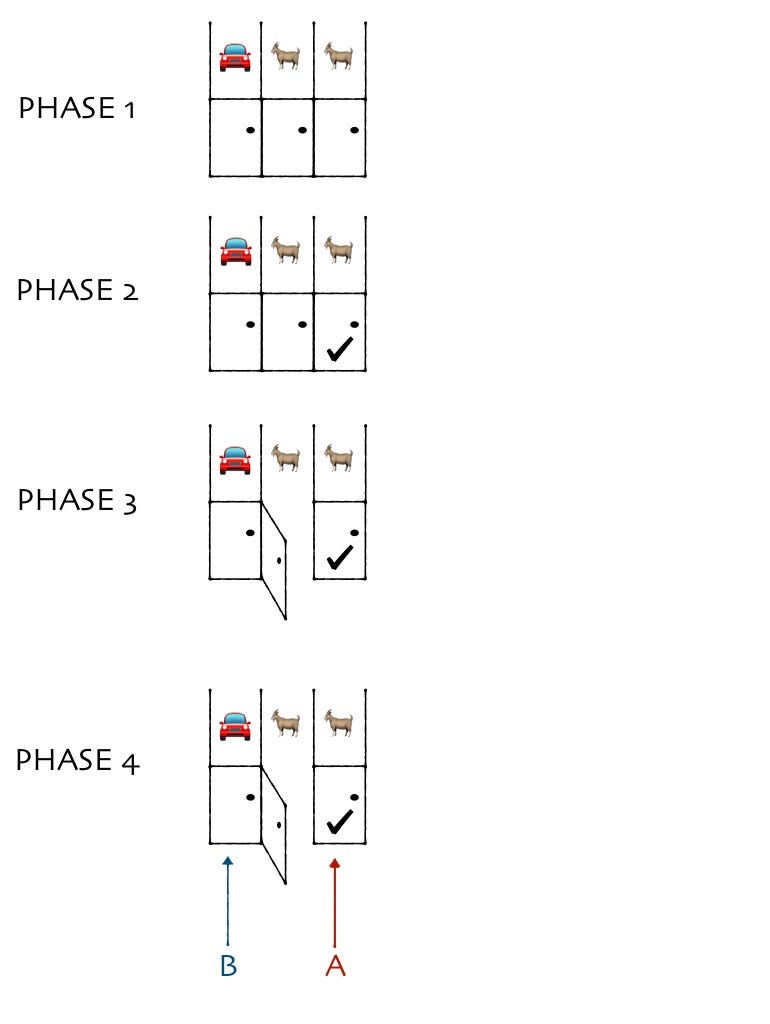
There are 3 doors. A car is randomly placed behind one, and goats behind the other 2.
You pick one door.
Monty looks behind the other 2 doors. He chooses one of them with a goat behind it, and opens it.
You get two options:
Option A: You get whatever is behind the door you picked.
Option B: You get whatever is behind the other closed door.
The well-known solution is that you should always switch, which gets you the car 2/3 of the time.
Variant
In our variant, Monty is corrupt. The night before the game, you show up at his house with a suitcase of cash. He agrees that he will follow whatever algorithm you want when choosing the door to open. (Of course, he still can't open a door with a car.)
What makes this challenging is:
Monty doesn’t know where the car will be before the show starts.
After the show starts, Monty can’t communicate with you other than by choosing what door to open.
The problem is: What is the best strategy for you and Monty to use? And if you use that strategy, how likely are you to get the car?
Thoughts
The naive solution would be to play as if there was no conspiracy: If Monty picks a random door to open and you always switch, then you get the car 2/3 of the time. The question is: Can you do better?
I’m pretty sure I have the answer, but people always yell at me when I talk about this stuff I don’t yet have an elegant proof.
Do you have one? If so, please send it to me. When/if I get some nice solutions, I’ll post an update.


I don't think you can do better than the naive solution.
Two thirds of the time, Monty's hands are tied: that's what yields the traditional solution. When his hands aren't tied, he doesn't have an avenue to communicate the difference between "I have to pick this door" and "We conspired to pick this door".
I think a clever thing about this variation is that it re-introduces a 50/50 likelihood in a manner similar to the false intuition of the original problem. If you conspire to pick a specific door under the scenario when you have already chosen the car, then when Monty selects that door it really is 50/50 for keeping your choice or switching.
I've verified this via Monte Carlo simulation, but I'd be very happy to be proven wrong. I'm one of the people who's lost productivity to this problem. :)
I don't think this is doable. To my understanding the only thing that matters is what Monty does when you pick the car, and therefore an algorithm comes down to where he picks when you pick car.. There are other ways to get to 2/3, i.e. "if I pick the car, always pick the one on the right", but fundamentally you always provide as much false information as true information. I imagine you might have some probabilistic solution but I am skeptical it will work.
1/3 You pick the Car, he is free to tell you to hold, you win.
1/3 You pick a Goat, he has no choice which door to open but it corresponds to switch, you win.
1/3 You pick a Goat, he has no choice which door to open but it corresponds to hold, you lose.