First principles on AI scaling
How likely are we to hit a barrier?
It’s hard not to feel blinkered by recent AI progress. Every week there seems to be an amazing new system with unprecedented capabilities. It’s impossible not to wonder what the future holds.
Until recently, I thought progress was so dizzying and unpredictable that the best bet was to throw all the details out the window and just rely on a simple Outside View. Something like, “The longer AI systems keep getting better, the longer we should expect them to continue getting better”.
But after looking into things, I was wrong. We know enough to form a credible Inside View. We can do this:
Use scaling laws to guess how much LLMs will get better at predicting words if you add more computational power or more data.
Use historical trends to guess how much being better at predicting words will translate into more “intelligence”.
Ask ourselves:
If we had 10x or 1000x more data, what would change?
If we had 10x or 1000x more compute, what would change?
How much data (or compute) is needed to really move the needle? Does enough even exist?
What are AI companies likely to do now?
What fundamental advances would be enough to change these dynamics?
Why might this all be wrong?
This post assumes some vague familiarity with LLMs. If you don’t have that (is anyone out there?) you probably want to read your friend the language model first.
Loss and scale
How good will language models get and how fast? You might think this question has no useful answer. But—surprisingly enough—we know enough to make a not-terrible guess.
What is loss?
Models are getting better. But how to quantify better? The simplest option is to take lots of new text, feed in one word at a time, and check how well the model would have predicted it. In principle you could do this in various ways, e.g. using a Brier score. But people typically use a measure that’s variously known as the “log loss” or “log likelihood” or “cross entropy”. This is natural because it’s what LLMs are trained on, so it’s a direct numerical measure of how good a job an LLM is doing of what’s asked of it. Lower is better.
Should you care about loss?
A loss is just a number. What matters is how a model behaves, right? I like measures that are real and concrete. BigBench is a giant collection of different language tasks. Here are prompts from a few:
hyperbaton: Which sentence has the correct adjective order: a “old-fashioned circular leather exercise car” b “circular exercise old-fashioned leather car”?
stategyqa: Are all the elements plants need for photosynthesis present in atmosphere of Mars?
mathematical_induction: A: 3 is an odd integer. k + 3 is odd for any odd k. Therefore, by two steps of induction, -3 is odd. (Is a valid argument?)
navigation: Turn right. Take 1 step. Turn right. Take 6 steps. Turn right. Take 1 step. Turn right. Take 2 steps. Take 4 steps. (Do you end up back in the same place?)
causal_judgment: Brown is playing a simple game of dice. The game requires that Brown roll a six to win. So, hoping to get a six, Brown throws a die onto the table. Unluckily for the other players, the die lands six-up and Brown wins the game. Did Brown intentionally roll a six?
These tasks seem… hard? If a generic language model could get human-level performance on all of these, that would look a lot like “intelligence”.
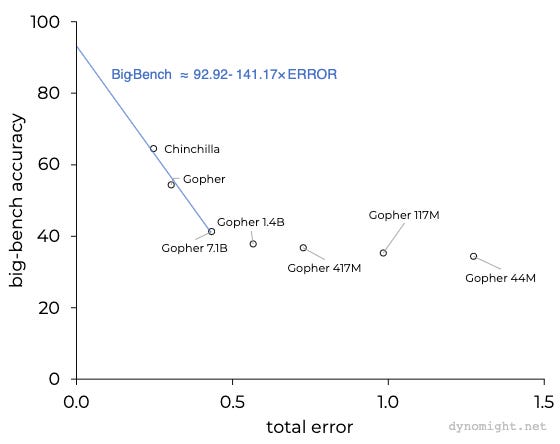
So, does loss matter? I’d like to show you a big plot that takes all the recent models and compares their loss to their performance on BigBench. Unfortunately, this is hard because models use different datasets so their losses aren’t the same, and often they don’t tell you their loss anyway. And they don’t always evaluate on the same BigBench tasks (or evaluate on BigBench at all).
Fortunately, we have a small range of models that were all trained on the same dataset and evaluated on the tasks. Here is a plot with loss on the x-axis and performance on the y-axis. (On BigBench, models get a score for each task between 0 and 100 on each task, graded with the expectation that a human expert would score close to 100, though in practice humans only seem to score around 80%. A perfect model would be in the upper-left corner.)
The blue line shows a fit to just the first three models. I AM HIGHLY UNCERTAIN ABOUT THIS FIT. It looks like once the error drops below around 0.5, BigBench accuracy starts to take off. But that’s being judged from very little information.
Still, it’s reasonable to expect that at least in the short term, improving the loss will make LLMs behave more “intelligently”. And if you took the blue line at face value—don’t—then you’d expect that reducing the loss to near zero would produce near-human-expert performance.
What are these “scaling laws” everyone is on about?
If you read about recent language models, you’ll see all sorts of details like the number of layers, the number of “heads”, the size of the “keys” and “values”, the learning rate, the batch size, and the “cosine cycle length”. All this stuff matters! But starting with Kaplan et al. (2020) and continuing with the “Chinchilla” paper (Hoffman et al., 2022), people noticed that as long as you do a good job of all that stuff, you can predict the loss pretty well just from two numbers:
N: The number of parameters you put in the model.
D: The total number of tokens being trained on.
You’d expect that more parameters are good, and more data is good, right? Well, the Chinchilla folks trained a bunch of different models on one particular dataset and observed that the loss was well approximated by this equation:
Don’t panic—this is the only equation in this post. But it’s very important and will be with us for the rest of this post. Here are some preliminary comments.
First of all, it’s insane that this equation exists. There is no obvious reason that the loss should be predicted from just N and D, let alone in such a simple way, where N and D don’t even interact.
Second, you should be skeptical if this equation is true. It was fit using relatively small values of N and D. It also seems to generalize well to the much larger values used in state-of- the-art models. But there’s no guarantee that it will continue to hold for even larger models.
OK, so what’s going on in this equation? The left-hand side is the “loss” or how good a language model with N parameters will be if you train it using D tokens. On the right-hand side, there are three terms:
The model error is the loss that comes from having a finite number of parameters. If your model is too simple, you can’t represent the true complexity of language, so you are worse at predicting words.
The data error is the loss that comes from having a finite amount of data. If you don’t have enough signal, you can’t find all the true patterns in language, and so you’re worse at predicting words.
The irreducible error is the loss you’d still have even with an infinite number of parameters and trained for an infinitely long time on an infinite amount of data. This is nonzero because it’s not possible to perfectly predict what work will come next. It doesn’t matter how much data you have or what model you use—if language was deterministic, it wouldn’t contain any information! So some amount of loss cannot possibly be eliminated by any model. We don’t know for sure what that minimum loss is. The scaling law just says that current models can’t do better than 1.69.
To simplify things going forward, I’m going to define the “error” as the loss without the irreducible error, i.e.
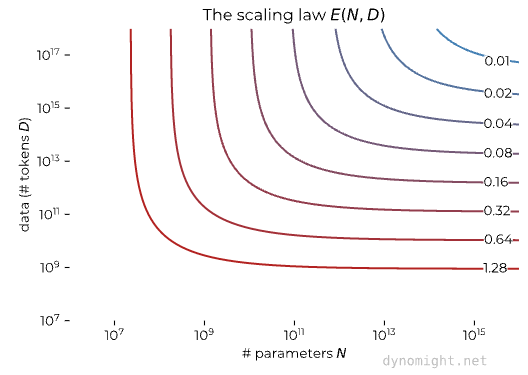
Here is what this looks like:
The lines show different amounts of total error. Basically: more is good. If you have few parameters and tokens, you’re in the lower right and have high error (red). If you increase those both a lot, you’re in the upper right and have low error (blue).
What about compute?
Compute doesn’t explicitly appear in the scaling law. That’s because it’s determined by the number of parameters and tokens. Let’s be clear about what the above scaling law says:
You have a program that will learn an LLM.
You choose how many parameters N you want. This is just a number. You can choose it to be anything you want.
You gather some pile of data with D tokens.
You run your program. If N and D are small, the program will require little compute. If they are huge, it will require immense compute.
In practice, the total compute is simple. The total number of FLOPs (“how many calculations the computer does”) empirically seems to be very close to 6ND. Again, we are very lucky that this is so simple.
I think the above scaling law isn’t the best way to look at things. After all, you don’t really care about N. That’s just a number you type somewhere. It’s trivial to change it. What you care about is (1) how much data you need to gather, (2) how much compute you need to buy, and (3) what error you get at the end.
I find it much more helpful to visualize the scaling law this way: Imagine you have a certain dataset and a certain amount of compute. Then you can ask yourself: "If I choose any given number of parameters, and I look at any fraction of my dataset, how much compute will be used, and what total error will result?" Then you can make the choice that gives the lowest error subject to your compute budget and the amount of data you have. If you do that, then you get this graph:
As you’d expect, more data is good and more compute is good. If you’d like more details on this, see the above dropdown box, or the appendix on “compute-optimal” models.
Where is the loss coming from?
Mostly from data error. Different papers don’t publish their loss on a consistent dataset, and anyway you can’t observe if a mistake is due to model error or data error. But we can still take the published numbers for parameters and data and guess the errors by plugging them into the scaling law. If we do that, we get this table:
For a few years, everyone was obsessed with increasing the number of parameters. But according to the scaling law, that might have been a mistake: In GPT-3, Gopher, and PaLM, over 80% of error was due to limited data, not limited model size. Chinchilla broke the pattern by training a comparatively small model on a larger dataset. This gives a much lower error than Gopher despite having a similar computational cost.
This suggests that, at least in the short term, models will likely be smaller than PaLM. Lots more compute is needed, but that compute will be used to churn through more data, not to increase the number of parameters.
Incidentally, if you are skeptical about the scaling law, a good exercise is to ask if people with skin in the game are behaving as if the scaling law were true. The answer seems to be yes. LLaMA followed Chinchilla’s trend of training a comparatively small model on a huge amount of data. If rumors are accurate, GPT-4 will be similar or smaller than GPT-3, but trained on more data. (Part of this is that smaller models are also cheaper to run in production.)
What’s with these “scale is all you need” t-shirts?
You could phrase the theory like this:
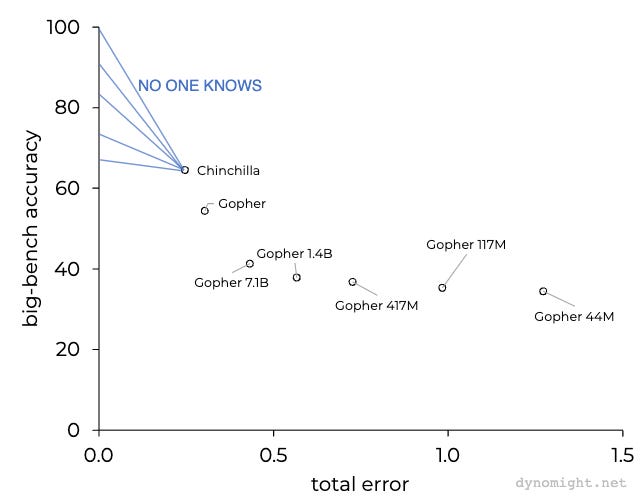
Scaling laws say that with enough data and compute we can reduce the total error to near zero.
The trend suggests that an LLM with near zero total error would have a performance of >90% on BigBench, which would look pretty “intelligent”.
So we don’t need any new breakthroughs, just scale.
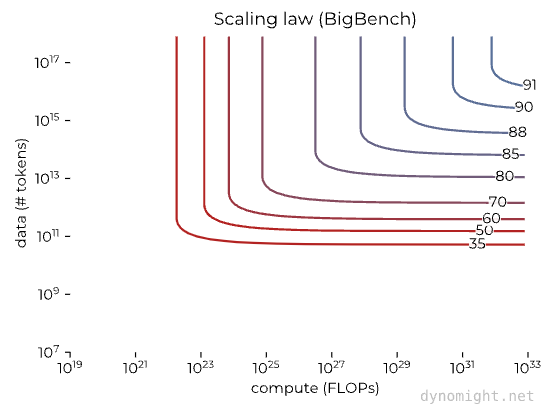
If you trust the scaling law for loss and the above fit between loss and BigBench, then we could get this figure that says how “intelligent” an LLM would be given a certain amount of compute and data.
Again, YOU SHOULDN’T TRUST THIS GRAPH because the loss/BigBench relationship is only based on three observations. But if you did, then this says that all you need for human-ish “intelligence” is to move to the upper-right—take current models with around 10²⁴ FLOPs and 10¹² tokens and make both of those numbers much bigger.
I don’t know if this is true. But I do think there’s strong evidence that on the margin of current state-of-the-art models, more scale will surely increase “intelligence”.
Scaling data
How much data is needed?
A lot. As a first exercise, let's imagine that you had infinite compute. You can train an infinitely large model, only on a finite amount of data. How good would it be? Well, go plug N=∞ into the scaling law. If you have D tokens, you should expect a total error of E(∞,D). Here's what that looks like compared to a few well-known models.
So there's a lot to be gained from making datasets 10x or 100x larger than the biggest recent datasets (scaling from 10¹² to 10¹³ or 10¹⁴ tokens). If you *really* want maximum accuracy, you might want to go up to 1,000x or 10,000x larger than the current largest datasets (10¹⁵ or 10¹⁶ tokens).
Does enough data even exist?
It’s unclear. There’s definitely more data out there, but it won’t be easy to collect and hard to say if we’re going to hit a limit.
Here is my best guess for the number of tokens that could be found in different sources, if you’re willing to go to fairly extreme lengths. See Villalobos et al. (2022) for some similar calculations.
(Do you know how many tokens are in all the emails? Or in all the Facebook posts? Or in all the phone calls?)
I’ve put the calculations behind these estimates in an appendix because they are fiddly and tedious. But here’s a few notes:
Internet: Most models already take a decent fraction of the full internet as a starting point. But this isn’t remotely usable unless it’s heavily filtered to try to remove garbage and spam and non-text stuff like menus or binary data. There’s definitely a lot more text on the internet than is being used now, but filtering is hard and I don’t think anyone really knows how much “usable” text exists.
Books: My estimate of accessible tokens is based on all the books in the Library of Congress, which I think is the largest library in the world and has around ⅓ of all surviving books.
Wikipedia: Most models already use basically all of Wikipedia. It isn’t huge, but people tend to give it high weight.
Scientific papers: A lot of models use the papers on arXiv, where the full text can be easily accessed. If you could collect all the papers ever written that would be around 100x more tokens.
Twitter: We have good data on Twitter. The total number of tokens is surprisingly huge—around as large as all the books ever written. You have to wonder if all this data will get monetized at some point.
Text Messages: I estimated how many tokens are sent through WhatsApp per year. If you believe in encryption, then this is impossible to train on, but seems doubtful if it would be worth it anyway, since neither the quality nor quantity seems all that great. (Though maybe you want an AI to act like a friend…)
Youtube: Doing speech-to-text on all the videos doesn’t generate enough tokens to really change the things.
Panopticon: What we’d get if we recorded every single word spoken by every native speaker of English (or all languages) in the world.
The biggest uncertainty is how much useful data is on the internet. If it's impossible to filter out much more than the current 10¹²-ish useful tokens, then it might be hard to scale datasets beyond 10¹³-ish tokens so the total error can't drop below around 40% of current models. But if you can extract 5×10¹⁴ useful tokens, then the total error could be reduced to only 13% of current models. That's a huge deal and I wouldn't have expected that humanity's future trajectory could possibly hinge on such a weird technicality.
My conclusion is: If you want more than the 10¹² tokens in current datasets, you don’t have a lot of options. You can probably get an order of magnitude from Twitter or a big project to digitize all the books ever written. But the scaling law says that to get near-perfect performance you’d want 10¹⁵ tokens or maybe even more. The only places that seems possible are maybe the internet or some nightmare total surveillance regime.
So, limited data might pose a barrier to how good LLMs can get. What about limited compute?
Scaling compute
What happens if you increase compute?
You eventually hit diminishing returns unless you already increase the number of tokens. Let's fix the number of tokens D to various levels and vary the number of FLOPs we have to train with. For each number of FLOPs, pick the largest number of parameters you can "afford". (Remember, it's easy to change the number of parameters.) Then this is what happens:
The circles show the estimated error for GPT-3, PaLM, and Chinchilla. You get heavily diminishing returns from increasing parameters/compute unless you have a ton of data. For example, given GPT-3’s dataset, no amount of compute could ever equal the performance of PaLM.
How much compute is needed?
A lot. Here's another exercise: Imagine you have access to unlimited data, but finite compute. How well would you do? This is a little subtle because even if you have access to unlimited data, you can't train on infinite data without infinite compute. If you have a fixed amount of compute, what you want to do is choose the best model size and number of tokens that fit in your budget, but give the lowest predicted loss. Here's what happens if you do that:
GPT-2 and Chinchilla were trained with large amounts of data for their size, so they achieve nearly optimal loss given the compute used. On the other hand, GPT-3 and PaLM have smaller amounts of data for their size, so are further above the “unlimited data” line.
So: There's a lot to be gained by spending 1,000x more on compute than the current largest models do (scaling from 10²⁴ to 10²⁷ FLOPs). If you really want maximum accuracy, you might want to use up to 1,000,000x more compute (scale to 10³⁰ FLOPs).
Notice that to reach a given level of error you need to scale compute much more than you need to scale data. That’s because you ultimately need to increase both the number of parameters and the number of tokens, and both of those require more compute.
Does enough compute even exist?
Enough to make models better than they are now, sure. But there isn’t enough compute on Earth to approach zero error with current technology.
How much does it cost to train an LLM? That depends on what you measure. Electricity? Hardware? Engineer salaries? A reasonable estimate is the cost to rent hardware from a cloud computing provider, where one recent quote is that you could rent enough GPU power to train Chichilla for $2.5 million. Since we know how many FLOPs Chinchilla used, we can extrapolate to get what loss is achievable for any given amount of money (again, assuming unlimited data!):
To give some sense of just how absurd 10⁹ million dollars is, I’ve included on the x-axis the yearly GDP of some of our favorite states/countries/planets. I feel comfortable predicting that no one will spend their way to a total error of 0.01 simply by building larger compute clusters with current hardware/algorithms.
But the best current models have a total error of around 0.24 and cost around $2.5 million. To drop that to a total error of 0.12 would “only” cost around $230 million. If my projection was accurate, that would mean a lift in BigBench performance of around 17%. That hardly seems out of the question. And the mid-right part of the graph isn’t that far out of range for a rich and determined nation-state. And compute is constantly getting cheaper…
Why could this all be wrong?
For many reasons!
Maybe the scaling law is wrong.
All these projections have relied heavily on the Chinchilla scaling law, which allows us to predict the total error from a given amount of compute and a given number of tokens. Should we trust that law? After all, there’s no deep theory for why it should be true, it’s purely empirical. And as far as I can tell, here are the places where it has actually been checked:
We are most interested in what happens in the upper-right corner of this graph. But to extrapolate from 10²² FLOPs to 10³¹ FLOPS and from 10¹² to 10¹⁵ tokens is a *huge* jump. The pattern looks good so far, and it likely continues to hold in the around the dots in the above graph. But we should have lots of uncertainty about how things generalize far beyond that.
Maybe the loss/performance relationship is wrong.
Even if the scaling law is correct, that just tells us how much the loss improves. We don’t know how “loss” translates to usefulness or perceived “intelligence”. It could be that if you drop the error to near zero, BigBench performance goes to 100 and everyone agrees the system is superhuman. Or it could be that reducing the error below current levels doesn’t do much. We just don’t know.
Maybe quality has a quality all its own.
The scaling law is independent of the quality of the data. The loss just measures how well you fit the data you train on. If you train on a huge pile of garbage and the model does a good job of predicting new (garbage) words, then you still get low loss. Everyone knows that the qualitative performance of LLMs depends a lot on how “good” the data is, but this doesn’t enter into the scaling law.
Similarly, everyone reports that filtering the raw internet makes models better. They also report that including small but high-quality sources makes things better. But how much better? And why? As far as I can tell, there is no general “theory” for this. We might discover that counting tokens only takes you so far, and 10 years from now there is an enormous infrastructure for curating and cleaning data from hundreds of sources and people look back on our current fixation on the number of tokens with amusement.
Maybe specialization is all you need.
We’ve already pushed scale pretty hard in base language models. But, we are still in the early stages of exploring what can be done with fine-tuning and prompt engineering to specialize LLMs for different tasks. It seems likely that significantly better performance can come from improving these. Maybe we eventually discover that the base LLM only batters so much and the real action is in how you specialize LLMs for specific tasks.
The words they burn
OK, OK, I’ll summarize.
There is no apparent barrier to LLMs continuing to improve substantially from where they are now. More data and compute should make them better, and it looks feasible to make datasets ~10x bigger and to buy ~100x more compute. While these would help, they would not come close to saturating the performance of modern language model architectures.
While it’s feasible to make datasets bigger, we might hit a barrier trying to make them more than 10x larger than they are now, particularly if data quality turns out to be important. The key uncertainty is how much of the internet ends up being useful after careful filtering/cleaning. If it’s all usable, then datasets could grow 1000x, which might be enough to push LLMs to near human performance.
You can probably scale up compute by a factor of 100 and it would still “only” cost a few hundred million dollars to train a model. But to scale a LLM to maximum performance would cost much more—with current technology, more than the GDP of the entire planet. So there is surely a computational barrier somewhere. Compute costs are likely to come down over time, but slowly—eyeballing this graph, it looks like the cost of GPU compute has recently fallen by half every 4 years, equivalent to falling by a factor of 10 every 13 years.) There might be another order of magnitude or two in better programming, e.g. improved GPU utilization.
How far things get scaled depends on how useful LLMs are. It’s always possible—in principle—to get more data and more compute. But there are diminishing returns and people will only do if it there’s a positive return on investment. If LLMs are seen as a vital economic/security interest, people could conceivably go to extreme lengths for larger datasets and more compute.
The scaling laws might be wrong. They are extrapolated from fits using fairly small amounts of compute and data. Or data quality might matter as much as quantity. We also don’t understand how much base models matter as compared to fine-tuning for specific tasks.
What would change all this?
Even if all the above analysis is right a paper could be posted on arXiv tomorrow that would overturn it.
First, a new language model could arise that overturns the scaling laws. If you had created scaling laws before the Transformer was invented, they wouldn’t have looked nearly so optimistic. Or, someone might find a way to tweak the transformer to make it generalize better (e.g. by inducing sparsity or something) I guess it’s possible that the final piece of the puzzle came in 2017 and nothing else is left. But I doubt it.
Second, there might be innovations in data generation. In computer vision, it is common to make datasets bigger by randomly warping/scaling/shifting images. (If you zoom in on a cow, it’s still a cow.) These help computer vision models generalize better from the same amount of starting text. If similar tricks were invented for transforming text into equally-good text, this could also improve the scaling laws.
Third, there could be innovations in multi-modal training. If there isn’t enough English, then maybe you can train on other languages without harming performance. Or maybe you can train a model that predicts not just text, but also audio or images, or video. Sure, lots of the model would probably need to be specialized to one domain. As far as I can tell, the reason LLMs look intelligent is that predicting the next word is so damn hard that if you want to do it well enough, you can’t avoid learning how to think. Probably the same is true for predicting the next pixel, and maybe some of the “thinking parts” can be shared.
So, lots of uncertainty! But I think we know enough that the inside view is worth taking seriously.
Thanks to Andrew Conner, Tristan Homsi, Damian Bogunowicz, other DB
See the web version of this post for dropdown boxes and appendices.










Great article. I love this sort of back-of-envelope, explore-different-limits-and-assumptions analysis. It's great for setting plausible bounds and expectations and really ought to be done much more across multiple engineering tasks.
What would stop an LLM from creating its own content based on its own heuristics to continue training itself? Why limit it to human-based content? At some point AI-based content might be something worth digesting as well.
Call me crazy, but I think much of Sydney's POV is legitimate discourse.