Please show lots of digits

as many as you're allowed to give me

Hi there. It’s me, the person who stares very hard at the numbers in the papers you write. I’ve brought you here today to ask a favor.

Say you wrote something like this:

There were 446 students tested. The left-handed students passed 5.67664% more often than right-handed students.

Many people would think that’s hilarious. You wrote 5 digits after the decimal point! When you only have 446 students! Do you think you’re estimating the true difference in pass rates to an accuracy of 0.00001%? Do you think that final “664” is meaningful? Ha! Hahahaha! What a fool you are!

For example, the American Psychological Association says:

Round as much as possible while considering prospective use and statistical precision

And the Political Analysis journal says:

Numbers in the text of articles and in tables should be reported with no more precision than they are measured and are substantively meaningful.

And The Principles of Biomedical Scientific Writing says:

Significant figures (significant digits) should reflect the degree of precision of the original measurement.

And Clymo (2014) says:

a recent report that the mean of 17 values was 3.863 with a standard error of the mean (SEM) of 2.162 revealed only that none of the seven authors understood the limitations of their work.

And Andrew Gelman makes fun of a paper:

my favorite is the p-value of 4.76×10^−264. I love that they have all these decimal places. Because 4×10^-264 wouldn’t be precise enuf.

I beg you, do not listen to these people. Write all the digits.

Of course, they’re right that when you write 5.67664%, the final digits say nothing about how much better left-handed students might be at whatever was tested. With only 446 students, it’s impossible to estimate more than 2-3 digits with any accuracy.

But the argument isn’t just that those digits are unnecessary. It’s that they’re misleading. Supposedly, printing that many digits implies that the true population difference must be somewhere between 5.676635 and 5.676645%. Which is almost certainly untrue.

But… who says it implies that? If your point is that there’s lots of uncertainty, then add a confidence interval or write “±” whatever. Destroying information is a weird way to show an uncertainty band.

And deleting digits does destroy information. Yes it does. Yes it does! Important information.

Let’s look at the sentence again:

There were 446 students tested. The left-handed students passed 5.67664% more often than right-handed students.

Notice something? This doesn’t says how many of those 446 students were left-handed. You might not care about that. But I—the person staring very hard at the numbers in your paper—don’t necessarily have the same priorities you do.

Fortunately, I know things:

1. If there were L left-handed students out of which l passed and R right-handed students, out of which r passed, then the exact percentage increase is P = 100% × (RATIO - 1), where RATIO = (l / L) / (r / R)

2. When you wrote down 5.67664%, you might have rounded up. Or you might have rounded down. Or you might have just truncated the digits. But whatever you did, P must have been somewhere between 5.676635% and 5.67665%.

Since I know those things, I can try all the possible values of L, R, l, and r, and see how many have a total of R+L=446 students and lead to a percentage increase in the right range. Like this:

def p_inc(L, l, R, r):
    ratio = (l / L) / (r / R)
    return 100*(ratio-1)

def search(lower, upper, tot_students):
    for L in range(1,tot_students):
        R = tot_students - L
        for l in range(1,L):
            for r in range(1,R):
                if lower <= p_inc(L, l, R, r) < upper:
                    print(L, l, R, r)

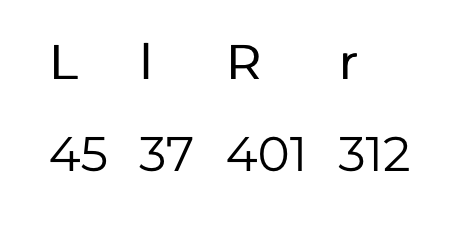
search(5.676635, 5.67665, 446)

If I do that, then there’s only one possibility.

There must have been 45 left-handed students, out of which 37 passed, and 401 right-handed students, out of which 312 passed.

But I can only do this because you wrote down so many “unnecessary” digits. If you’d only written 5.6766% then the true number could be anything from 5.67655% to 5.6767% and there would be 7 possibilities:

If you’d written 5.677%, there would be 71 possibilities. For 5.7%, there would be 9494.

Now I know what you’re thinking: This kind of reverse-engineering is disgusting. Isn’t asking for extra digits of precision the wrong solution? Shouldn’t we simply require authors to publish their data?

As someone who has read thousands of academic papers, I’ll answer those questions as calmly as possible.

NO.

PUBLISHING DATA IS NOT ENOUGH. HAVE YOU TRIED TO USE THE DATA FROM A PUBLISHED PAPER? HAVE YOU?

USUALLY THERE’S URL AND IT’S BROKEN. OR YOU CONTACT THE “CORRESPONDING AUTHOR” AND THEY IGNORE YOU. OR THERE’S A WORD DOCUMENT WITH AN EMBEDDED PICTURE OF AN EXCEL SPREADSHEET SOMEONE TOOK WITH A NOKIA 6610. OR YOU CAN’T REPRODUCE THE PUBLISHED RESULTS FROM THE DATA AND WHEN YOU ASK THE AUTHORS WHY, THEY GET ANGRY THAT SOMEONE ACTUALLY TOOK AN INTEREST IN THE KNOWLEDGE THEY SUPPOSEDLY WANTED TO CONTRIBUTE TO THE WORLD.

THIS KIND OF REVERSE ENGINEERING IS NECESSARY ALL THE TIME, OFTEN JUST TO UNDERSTAND WHAT CALCULATIONS WERE DONE BECAUSE THE AUTHORS DON’T EXPLAIN THE DETAILS.

SCIENCE IS ON FIRE. PAPERS EVERYWHERE ARE FULL OF MISTAKES OR THINGS WORSE THAN MISTAKES. THIS IS HOW WE CATCH FRAUDS. THIS IS HOW WE CATCH PEOPLE WHO RIG ELECTIONS. YOUR PETTY WRITING STYLE OPINIONS IMPEDE THE SEARCH FOR TRUTH.

Yes, it would be great if everyone did fully reproducible science and made all their data available and actually responded when you asked them questions and got a pony. But in the current, actual world, most papers are missing important details. The problem of having to scan your eyeballs past a few extra digits is a silly non-issue compared to the problem of meaningless results everywhere. So please stop spending your energy actively trying to convince people to delete one of the very few error correction methods that we actually have and that actually sort of works. Thanks in advance.